Basic, Mandelbrot et flocon de neige

Image : Evercat

J'ai découvert l'informatique au tout début des années 80, dans un cours pour enfants de la MJC de Sceaux. Nous étions dotés d'Apple II.


A l'époque, commencer l'informatique, c'était apprendre le langage BASIC. C'était apprendre à programmer des boucles élémentaires pour mettre au point de petits jeux ou pour tracer de jolies courbes sur l'écran.


C'est à ce moment que j'ai pour la première fois entendu parler de fractales et de courbes de Mandelbrot. Parce que les fractales et les courbes de Mandelbrot, c'est beau et ça se programme sans grande difficulté en BASIC (en tous cas en 2 D).


Vous pouvez admirer des milliers d'images fractales en 2 D ici. 

Auteur : Jean-Christophe Michel : http://framy.free.fr

Les fractales sont des fonctions mathématiques aux propriétés surprenantes. La plus connue est l'autosimilitude. Elle signifie  que leur complexité est invariante par changement d'échelle. Autrement dit, en termes prosaïques, que l'on observe une section de la courbe sur une grande échelle ou une petite échelle, on retrouve toujours le même dessin.

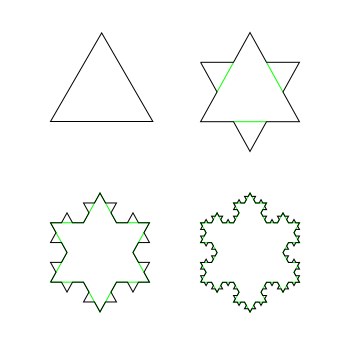
L'exemple classique de ce phénomène est le flocon de neige. Quelle que soit l'échelle à laquelle vous l'examinez, il présente toujours la même structure.Un exemple, ci-dessous :

Flocon de Koch - Auteur de l'image animée : Christophe Dang Ngoc Chan

La théorie mathématique qui sous-tend ces courbes dépassait de loin les capacités de mon cerveau d'enfant. Elles dépassent encore de très loin - de plus loin encore ? - les capacités de mon cerveau d'adulte. Pour ceux qui veulent creuser la question, l'article de Wikipedia est assez bien fait.

L'auteur de cette théorie, Benoit Mandelbrot, est mort jeudi dernier, le 14 octobre. 

Par la beauté de ses courbes, il m'a fait pencher vers la science et m'a fait aimer l'informatique. Mon incapacité à comprendre en profondeur les maths m'a orienté vers le droit. C'est ainsi que je dois pour partie à Benoit Mandelbrot d'être devenu avocat amateur de science et de technologies. Il ne l'a jamais su évidemment..

Je tenais à lui en rendre hommage.

Marc Lipskier